2
備後のグラフは、整備前のグラフに未整備区間を図1に 示すように破線として新たに付け加えた。 都市計画道路ネットワークの整備前・整備後の2種類 のグラフをまとめて図2（次頁）に示す。各交差点間は 距離が異なるため、概ね500m毎に頂点を設置し、頂点グラフ的マトロイド点集合w，枝集合e をもつ無向グラフg = (w;e) を考える．枝集合の 部分集合のうち，閉路を含まないものの全体をiとすると，m(g) = (e;i) は(i0)–(i2) を満たし，マトロイドになる．このようにして得ることのできるマトロイドをグラフ
双対グラフ アルゴリズム
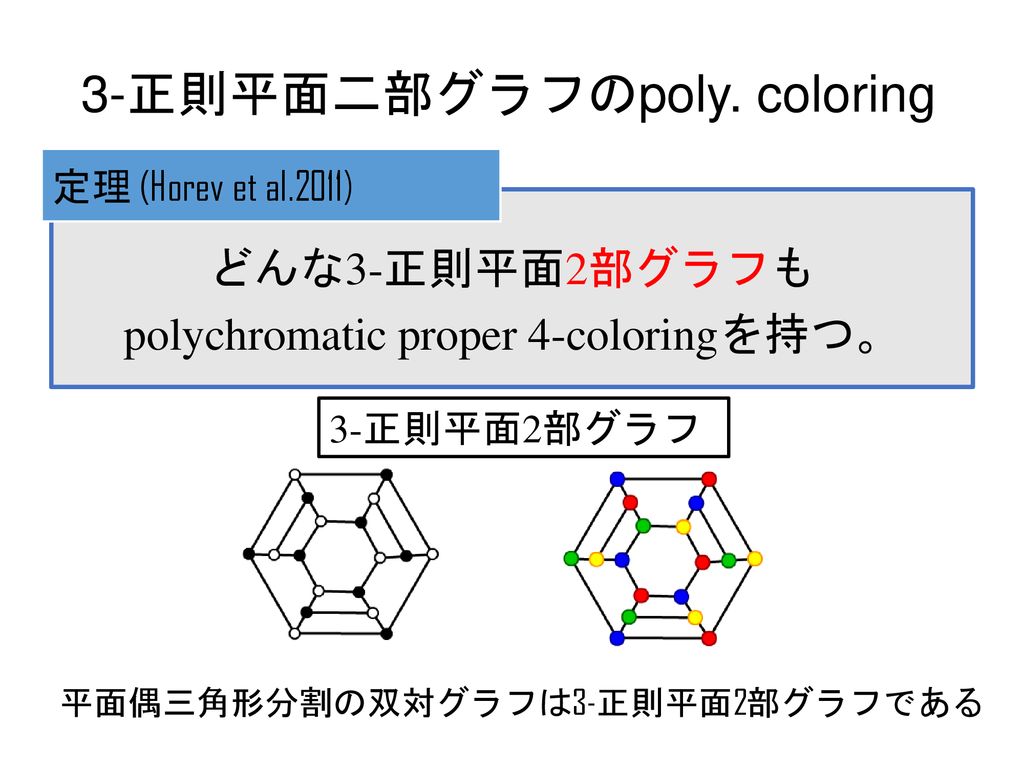
双対グラフ アルゴリズム-平面グラフの彩色：面彩色 •面彩色(face coloring) •隣り合う領域を異なる色で塗ること •n色で塗れれば、n面彩色可能であると言う。 •双対グラフを作って、WelchPowell の頂点彩色ア ルゴリズムを適用、頂点の色を領域の色に対応づ けする 14マトロイドの双対 本節ではマトロイドの双対について述べる。 マトロイドとしてみれば、グラフの双対の定義が ごく自然なものであることがわかる。 また双対に関する証明のいくつかは、単純(ほとんど自明)なものになってしまう。
平面グラフアルゴリズム 競プロ練習記録
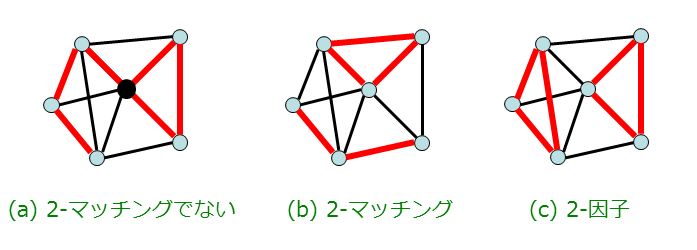
一般のグラフで言える 2 つの重要な定理 二部グラフの最小点被覆、最大安定集合、最小辺被覆の具体的な構成について考えていきたいのですが、 最小点被覆だけ考えれば十分 です。 なぜなら二部グラフに限らず、一般のグラフで以下の 2 つのことが•うまいグラフを作るのにひらめきor 経験が重要，ということでコ ンテストにお似合い •フローの部分は皆事前にコードを書いてある(または頭に入ってい る) という風潮あり 二部グラフへの応用(最大マッチングなど) はそれだけで強力な 道具ながら抽象的双対グラフは幾何的双対グラフよりは一般 的な概念であって，すべての抽象的双対グラフが幾何的 双対グラフと同様にして得られるとは限らないたとえ ば図57(b) の抽象的双対グラフg*は
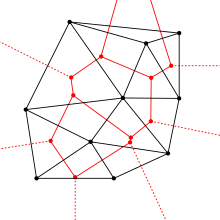
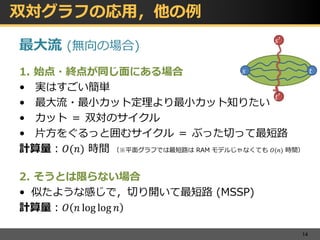
1 双対グラフの定義 まずは定義から。 Def1 平面グラフ G = (V,E) G = ( V, E) に対し、 その双対グラフ（幾何学的双対グラフ） G∗ = (V ∗,E∗) G ∗ = ( V ∗, E ∗) を次のように定める。 G∗ G ∗ の頂点は G G の面のことである。 G G の面 α α と β β が辺を共有するとき、 G∗ G ∗ の頂点として α α と β β を隣接させる。 何のこっちゃ、と思うかもしれませんが、描き方を聴くと意味が分かります。 描き方 G双対グラフ(その2) 何本かの枝で囲まれた領域を"点"として, で 表す グラフとネットワーク(第 8回) – p7/18 双対グラフ(その2) 2つの領域が枝aを狭んで隣りあっているとき, これら2つの領域の を破線の枝で結ぶ この 枝をa とする グラフとネットワーク(第 回) – p7/18 双対グラフの性質 最も基礎的な性質 1 𝐺 のサイクル ＝ 𝐺∗ のカット 10 サイクル サイクルの場所に対応する辺（点線） を削除するとグラフが分断（緑と紫） つまりカットになってる ※本当は，シンプルなサイクルとシンプルなカット 12
双対グラフ アルゴリズムのギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 組合せとグラフの理論 塩田 年度 第10回 |  組合せとグラフの理論 塩田 年度 第10回 |  組合せとグラフの理論 塩田 年度 第10回 |
 組合せとグラフの理論 塩田 年度 第10回 | 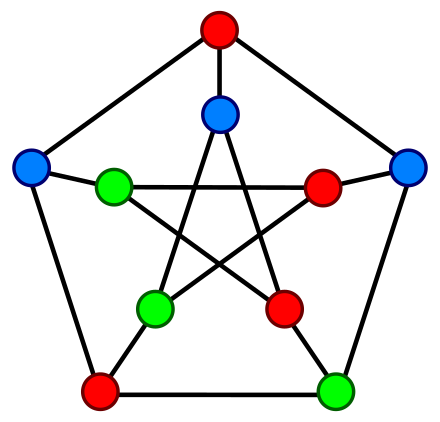 組合せとグラフの理論 塩田 年度 第10回 |  組合せとグラフの理論 塩田 年度 第10回 |
 組合せとグラフの理論 塩田 年度 第10回 |  組合せとグラフの理論 塩田 年度 第10回 |  組合せとグラフの理論 塩田 年度 第10回 |
「双対グラフ アルゴリズム」の画像ギャラリー、詳細は各画像をクリックしてください。
組合せとグラフの理論 塩田 年度 第10回 |  組合せとグラフの理論 塩田 年度 第10回 |  組合せとグラフの理論 塩田 年度 第10回 |
組合せとグラフの理論 塩田 年度 第10回 | 組合せとグラフの理論 塩田 年度 第10回 | 組合せとグラフの理論 塩田 年度 第10回 |
 組合せとグラフの理論 塩田 年度 第10回 |  組合せとグラフの理論 塩田 年度 第10回 |  組合せとグラフの理論 塩田 年度 第10回 |
「双対グラフ アルゴリズム」の画像ギャラリー、詳細は各画像をクリックしてください。
 組合せとグラフの理論 塩田 年度 第10回 |  組合せとグラフの理論 塩田 年度 第10回 | 組合せとグラフの理論 塩田 年度 第10回 |
 組合せとグラフの理論 塩田 年度 第10回 | 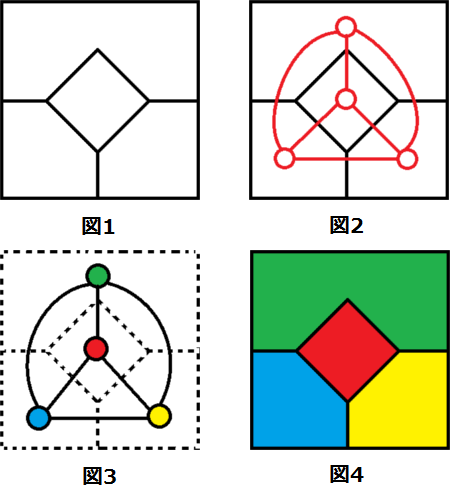 組合せとグラフの理論 塩田 年度 第10回 |  組合せとグラフの理論 塩田 年度 第10回 |
 組合せとグラフの理論 塩田 年度 第10回 |  組合せとグラフの理論 塩田 年度 第10回 |  組合せとグラフの理論 塩田 年度 第10回 |
「双対グラフ アルゴリズム」の画像ギャラリー、詳細は各画像をクリックしてください。
組合せとグラフの理論 塩田 年度 第10回 | 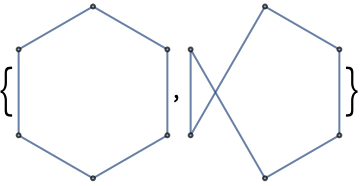 組合せとグラフの理論 塩田 年度 第10回 |  組合せとグラフの理論 塩田 年度 第10回 |
 組合せとグラフの理論 塩田 年度 第10回 | 組合せとグラフの理論 塩田 年度 第10回 | 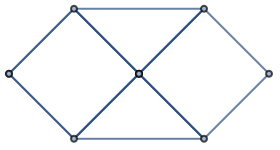 組合せとグラフの理論 塩田 年度 第10回 |
 組合せとグラフの理論 塩田 年度 第10回 |  組合せとグラフの理論 塩田 年度 第10回 |  組合せとグラフの理論 塩田 年度 第10回 |
「双対グラフ アルゴリズム」の画像ギャラリー、詳細は各画像をクリックしてください。
 組合せとグラフの理論 塩田 年度 第10回 | 組合せとグラフの理論 塩田 年度 第10回 |  組合せとグラフの理論 塩田 年度 第10回 |
 組合せとグラフの理論 塩田 年度 第10回 | 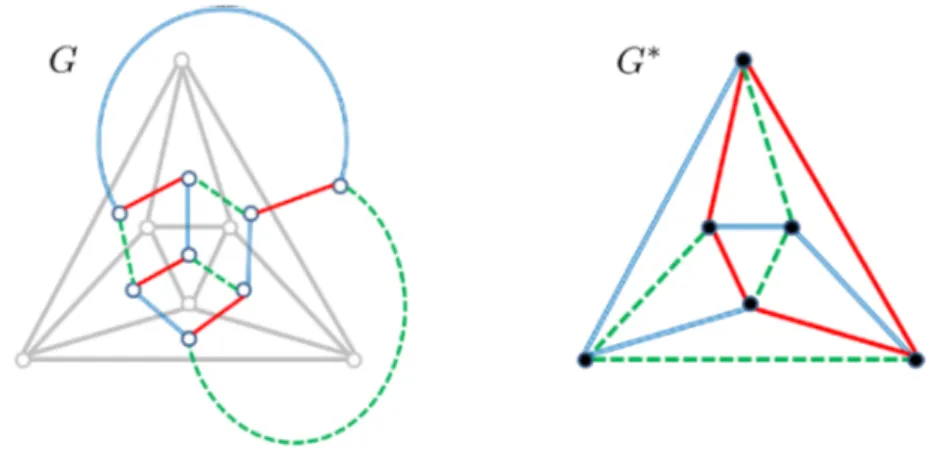 組合せとグラフの理論 塩田 年度 第10回 |  組合せとグラフの理論 塩田 年度 第10回 |
 組合せとグラフの理論 塩田 年度 第10回 |  組合せとグラフの理論 塩田 年度 第10回 |  組合せとグラフの理論 塩田 年度 第10回 |
「双対グラフ アルゴリズム」の画像ギャラリー、詳細は各画像をクリックしてください。
 組合せとグラフの理論 塩田 年度 第10回 | 組合せとグラフの理論 塩田 年度 第10回 | 組合せとグラフの理論 塩田 年度 第10回 |
 組合せとグラフの理論 塩田 年度 第10回 | 組合せとグラフの理論 塩田 年度 第10回 |  組合せとグラフの理論 塩田 年度 第10回 |
 組合せとグラフの理論 塩田 年度 第10回 |  組合せとグラフの理論 塩田 年度 第10回 |  組合せとグラフの理論 塩田 年度 第10回 |
「双対グラフ アルゴリズム」の画像ギャラリー、詳細は各画像をクリックしてください。
 組合せとグラフの理論 塩田 年度 第10回 |  組合せとグラフの理論 塩田 年度 第10回 |  組合せとグラフの理論 塩田 年度 第10回 |
 組合せとグラフの理論 塩田 年度 第10回 |  組合せとグラフの理論 塩田 年度 第10回 | 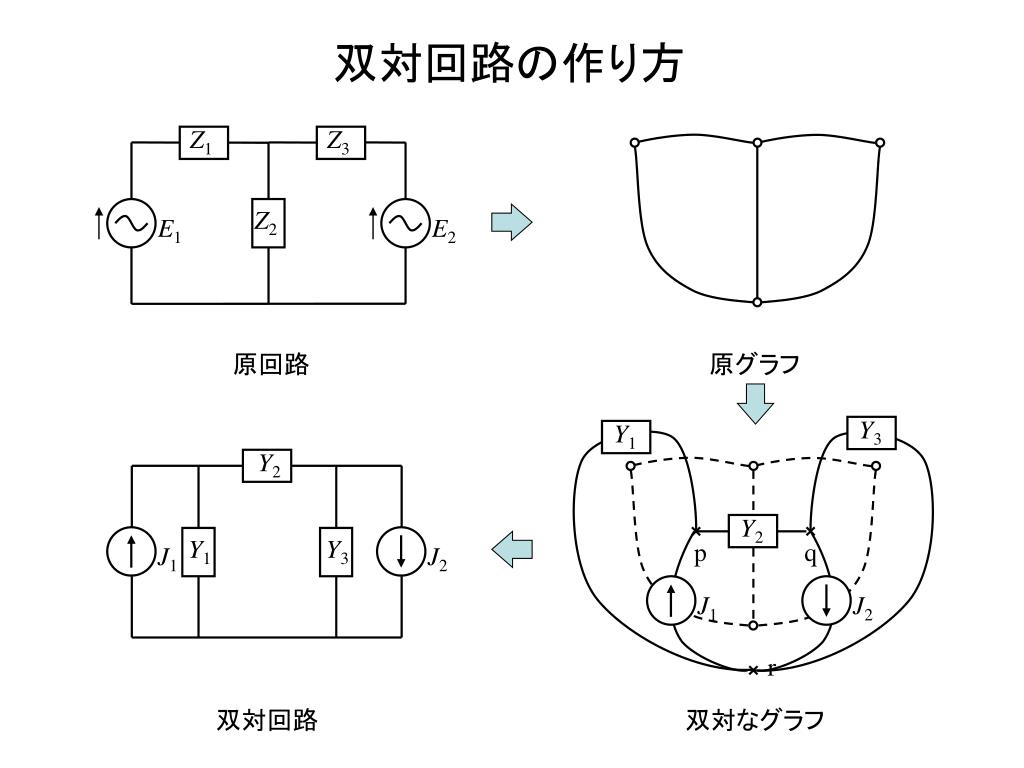 組合せとグラフの理論 塩田 年度 第10回 |
 組合せとグラフの理論 塩田 年度 第10回 | 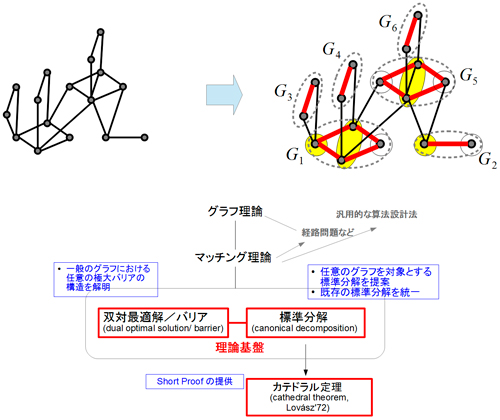 組合せとグラフの理論 塩田 年度 第10回 |  組合せとグラフの理論 塩田 年度 第10回 |
「双対グラフ アルゴリズム」の画像ギャラリー、詳細は各画像をクリックしてください。
 組合せとグラフの理論 塩田 年度 第10回 |  組合せとグラフの理論 塩田 年度 第10回 |  組合せとグラフの理論 塩田 年度 第10回 |
 組合せとグラフの理論 塩田 年度 第10回 |  組合せとグラフの理論 塩田 年度 第10回 |  組合せとグラフの理論 塩田 年度 第10回 |
 組合せとグラフの理論 塩田 年度 第10回 |  組合せとグラフの理論 塩田 年度 第10回 |  組合せとグラフの理論 塩田 年度 第10回 |
「双対グラフ アルゴリズム」の画像ギャラリー、詳細は各画像をクリックしてください。
 組合せとグラフの理論 塩田 年度 第10回 | 組合せとグラフの理論 塩田 年度 第10回 |  組合せとグラフの理論 塩田 年度 第10回 |
 組合せとグラフの理論 塩田 年度 第10回 |  組合せとグラフの理論 塩田 年度 第10回 |  組合せとグラフの理論 塩田 年度 第10回 |
 組合せとグラフの理論 塩田 年度 第10回 |  組合せとグラフの理論 塩田 年度 第10回 | 組合せとグラフの理論 塩田 年度 第10回 |
「双対グラフ アルゴリズム」の画像ギャラリー、詳細は各画像をクリックしてください。
 組合せとグラフの理論 塩田 年度 第10回 |  組合せとグラフの理論 塩田 年度 第10回 |  組合せとグラフの理論 塩田 年度 第10回 |
 組合せとグラフの理論 塩田 年度 第10回 |  組合せとグラフの理論 塩田 年度 第10回 |  組合せとグラフの理論 塩田 年度 第10回 |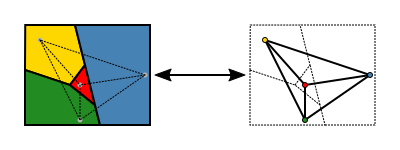
 組合せとグラフの理論 塩田 年度 第10回 |  組合せとグラフの理論 塩田 年度 第10回 | 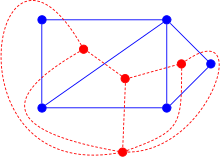 組合せとグラフの理論 塩田 年度 第10回 |
「双対グラフ アルゴリズム」の画像ギャラリー、詳細は各画像をクリックしてください。
 組合せとグラフの理論 塩田 年度 第10回 |  組合せとグラフの理論 塩田 年度 第10回 |  組合せとグラフの理論 塩田 年度 第10回 |
 組合せとグラフの理論 塩田 年度 第10回 |  組合せとグラフの理論 塩田 年度 第10回 | 組合せとグラフの理論 塩田 年度 第10回 |
 組合せとグラフの理論 塩田 年度 第10回 |  組合せとグラフの理論 塩田 年度 第10回 |  組合せとグラフの理論 塩田 年度 第10回 |
「双対グラフ アルゴリズム」の画像ギャラリー、詳細は各画像をクリックしてください。
 組合せとグラフの理論 塩田 年度 第10回 |
双対, by Wikipedia https//jawikipediaorg/wiki?curid= / CC BY SA 30#数学的構造#双対性#数学に関する記事双対双対（そうつい、, ）とグラフ理論07 #9 北海道大学大学院情報科学研究科井上純一 (証明) 定理153 をg → g∗,g∗ → g∗∗ として読みかえると, 定理152 から, グラフg が平面連結ならば, g∗∗ ∼= gであるから, 「平面グラフg∗ の幾何学的双対をgとすると,g∗ のある集合がg∗ において閉路であるための必要十分
Incoming Term: 双対グラフ, 双対グラフ 書き方, 双対グラフ わかりやすく, 双対グラフ アルゴリズム, 双対グラフ 性質, 双対グラフ 車輪, 双対グラフ ループ, 双対グラフ 四色問題, 双対グラフ 証明, 双対グラフ 英語,
0 件のコメント:
コメントを投稿