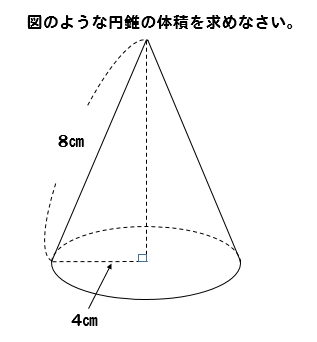
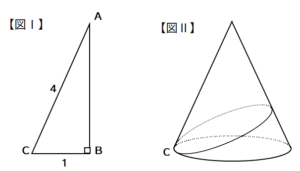
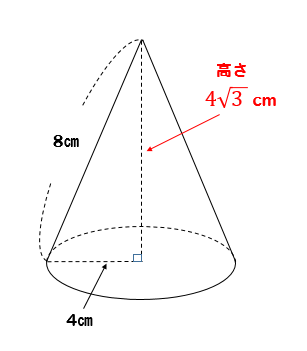
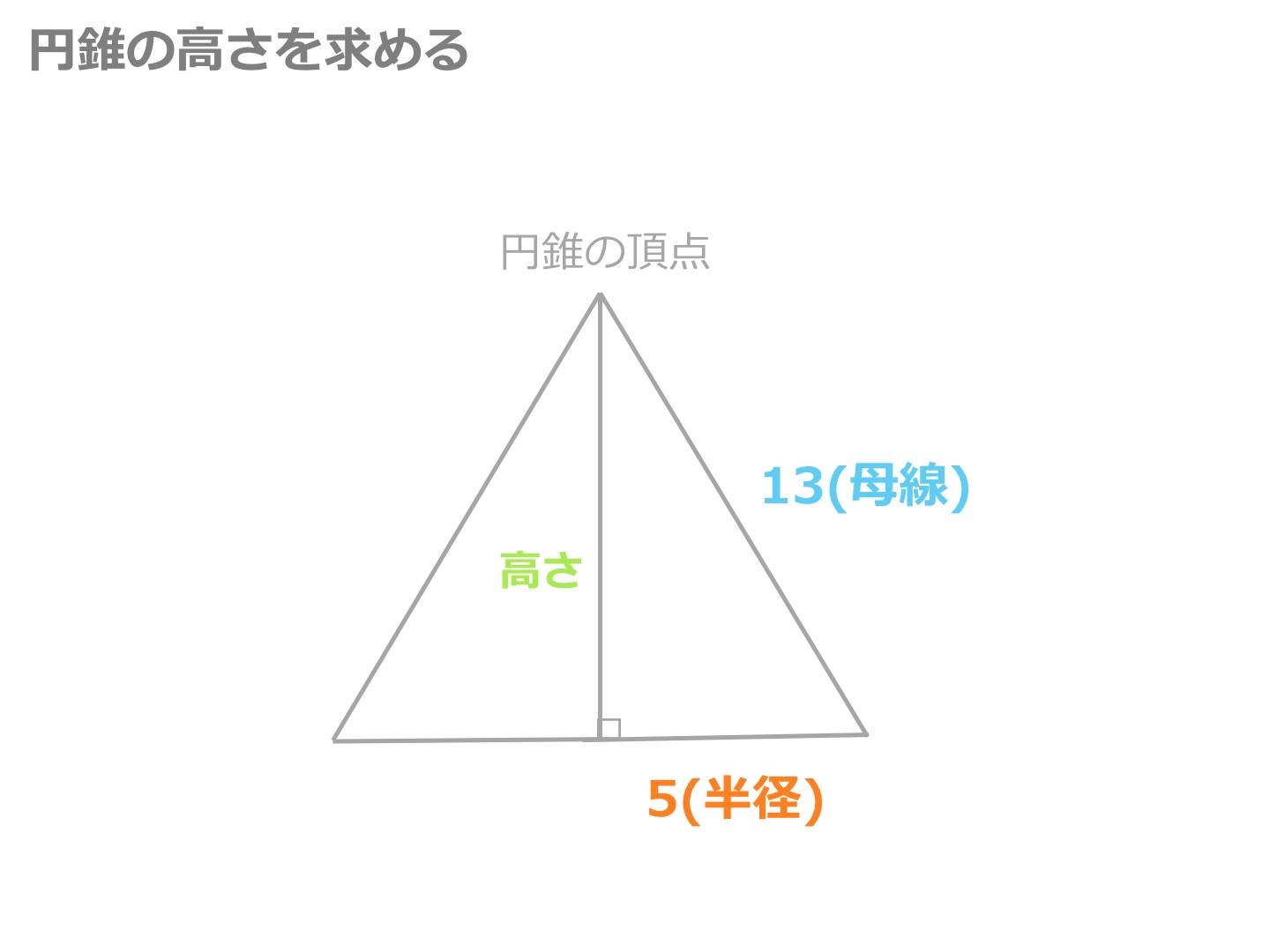
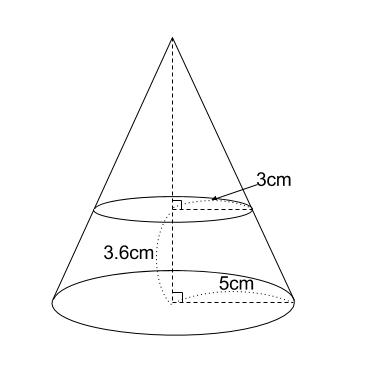
三平方の定理より、この円錐の高さ(下ろした垂線の長さ)は4になりますね。これで円錐の高さが求められました。 したがって、求める円錐の体積は、 3 2 π・4・1/3 = 12π・・・(答) となります。 半径と母線から円錐の高さを求めるテクニックはよく使用するので、知っておきま
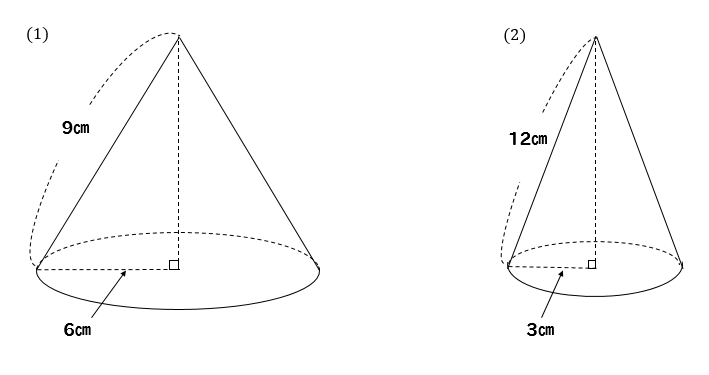
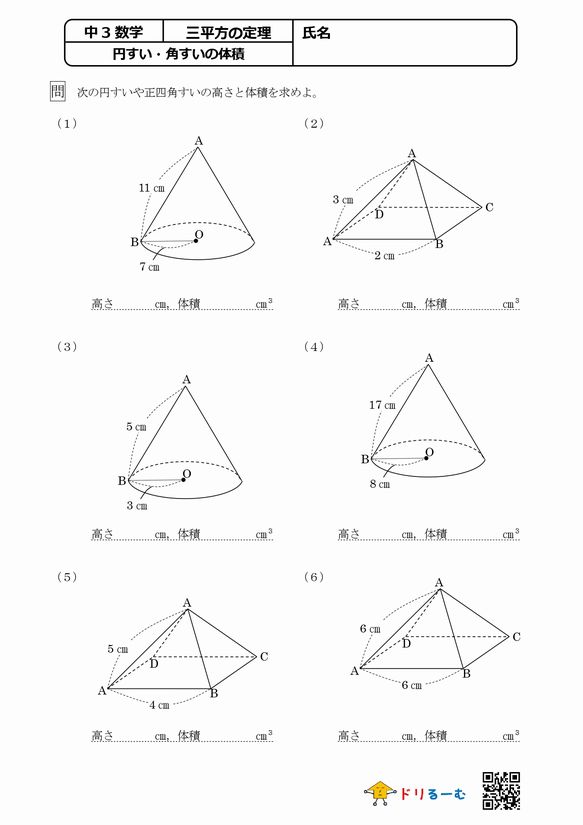
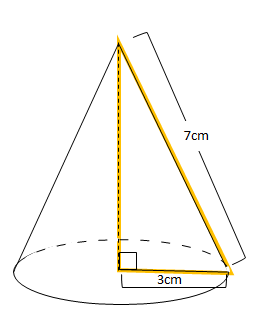
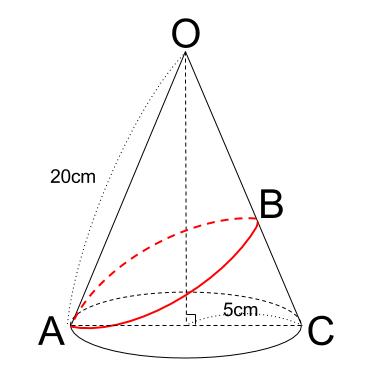
三平方の定理 円錐 高さ-三平方の定理5 (7)解説 図の円錐は底面の半径が6cm、 母線の長さが9cmである。 体積を求めよ。 母線の長さ9cm, 底面の半径6cm、円錐の高さをxとする。 三平方の定理にあてはめると x262=92 x2 = 45 x>0よりx=3 5 また、底面の面積は 6×6×π = 36π よって円錐の体積は 36π×3 5 ÷3 = 36 5 π 9 6 x 学習 コンテンツ 練習問題 各単元の要点 pcスマホ問題 数学の例題 学習アプリ 中2 連立方程式 計6 底面の半径が5cm,母線の長さが7cm の円錐について,次の問いに答えなさい。 ⑴ 円錐の高さを求めなさい。 ⑵ 円錐の体積を求めなさい。 x直方体の対角線の長さを cmとすると, 2 2x 2=6++5 x 2=125 x>0より,x=55 答 55cm 円錐の高さをhcm とすると, 5 2+h
三平方の定理 円錐 高さのギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 |  |  |
 |  | |
 | ||
 |  | |
「三平方の定理 円錐 高さ」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 | ||
 |  |  |
「三平方の定理 円錐 高さ」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 |  | |
 |  |  |
「三平方の定理 円錐 高さ」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
 |  |  |
「三平方の定理 円錐 高さ」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 | ||
 |  | |
 |  |  |
「三平方の定理 円錐 高さ」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
 |  |  |
「三平方の定理 円錐 高さ」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  |  |
 |  |  |
「三平方の定理 円錐 高さ」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
 |  |  |
 |  |  |
 |  |  |
「三平方の定理 円錐 高さ」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |
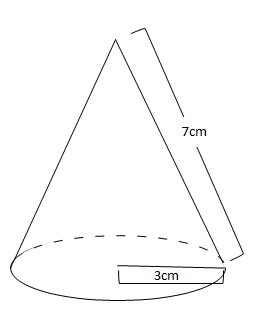
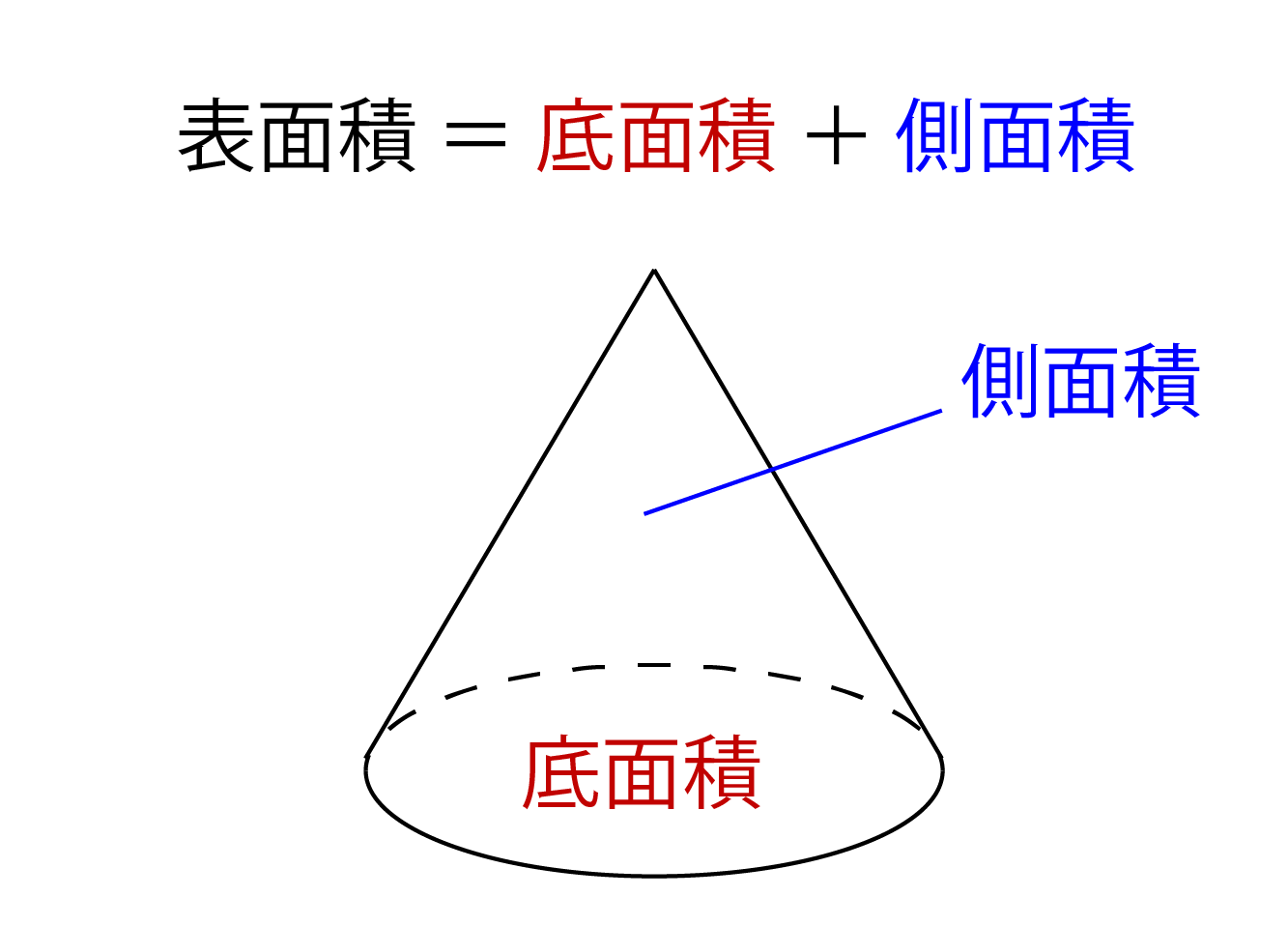
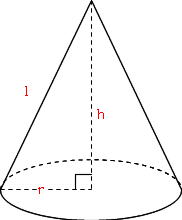
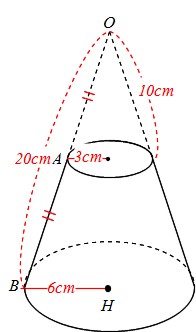
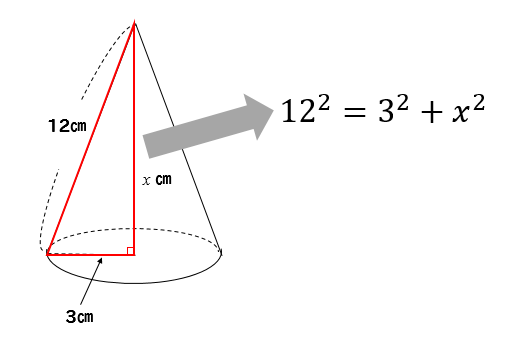
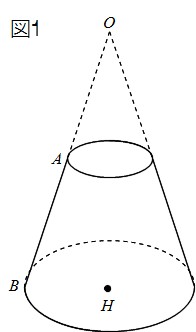
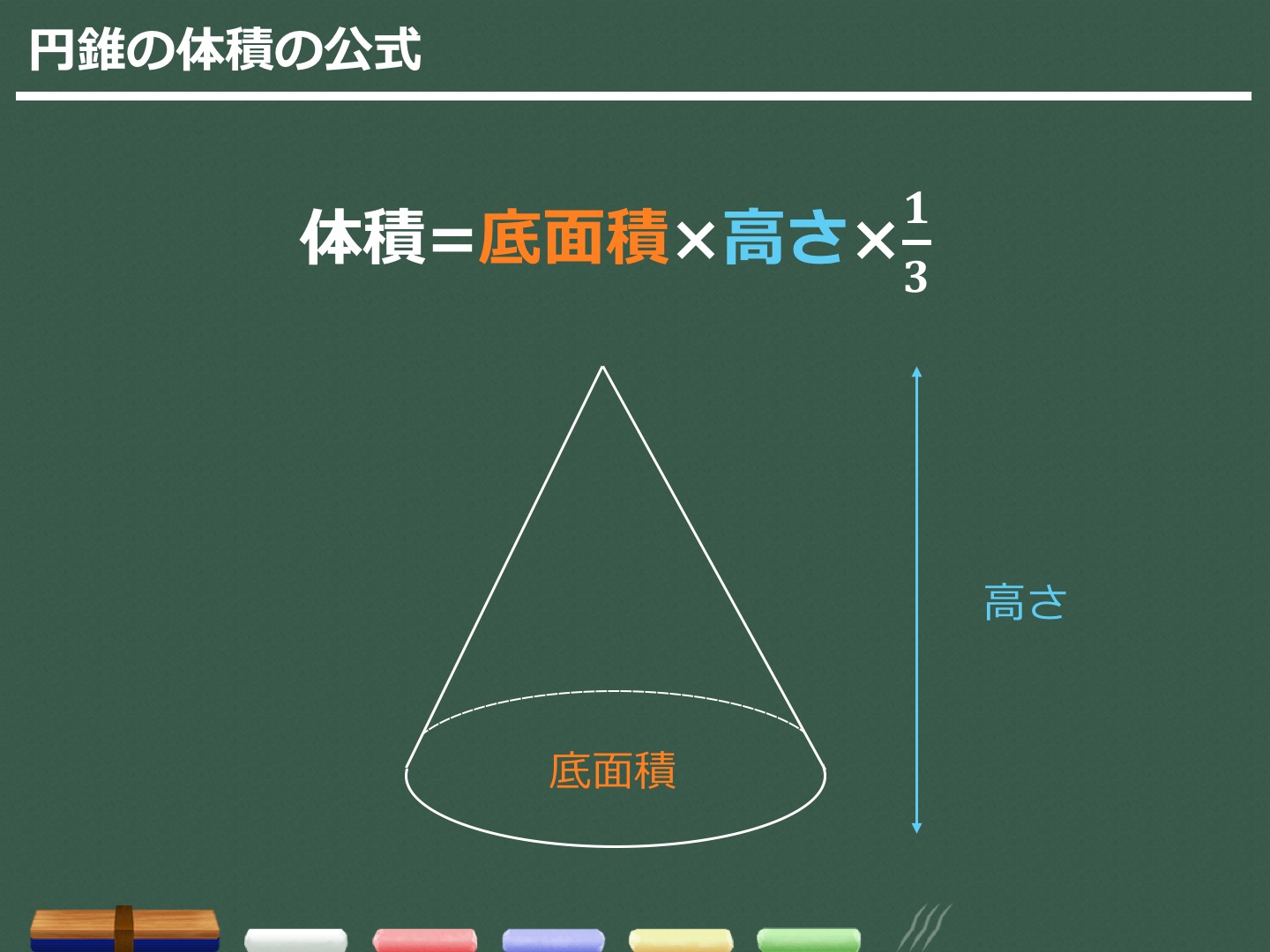
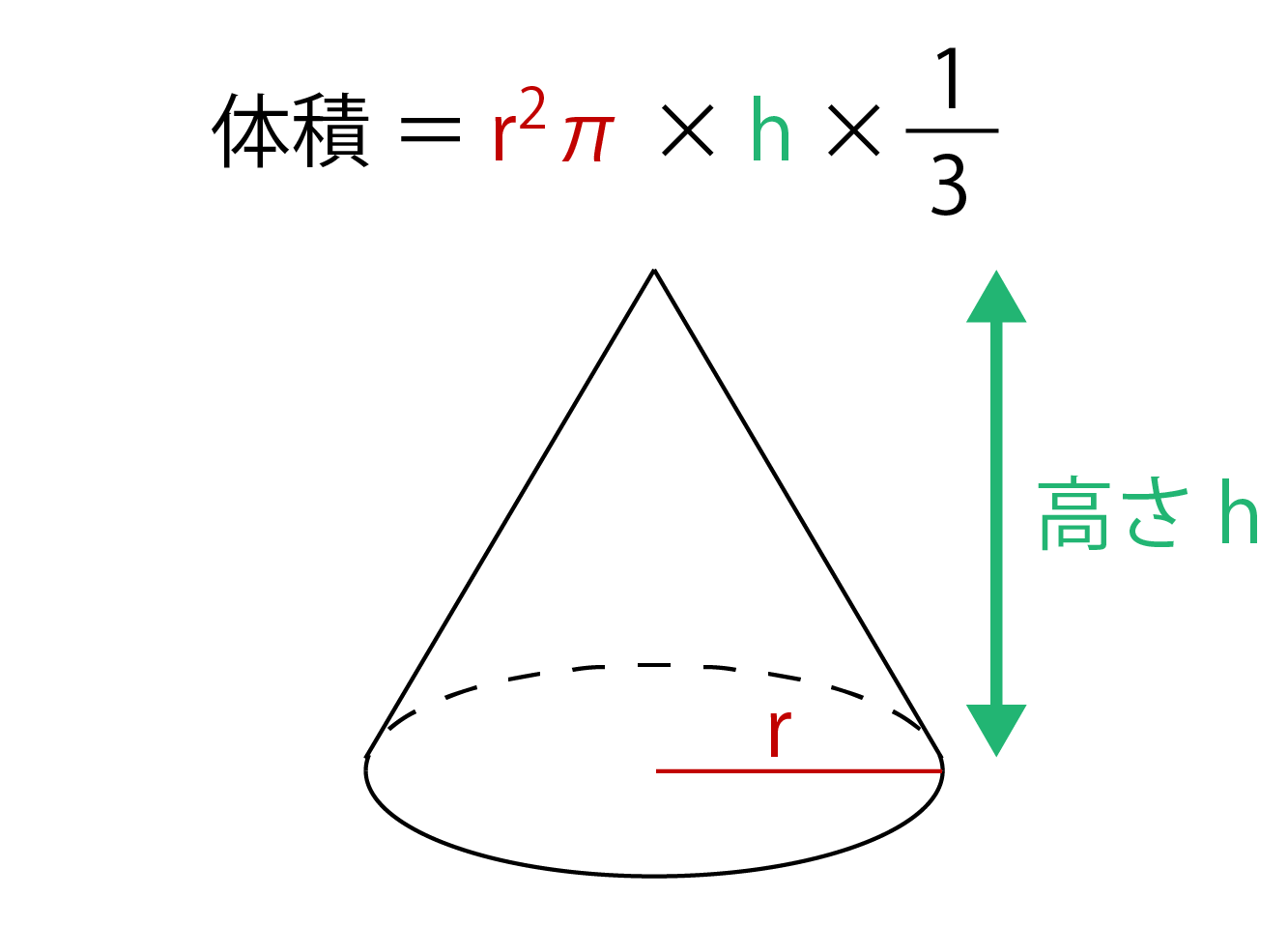
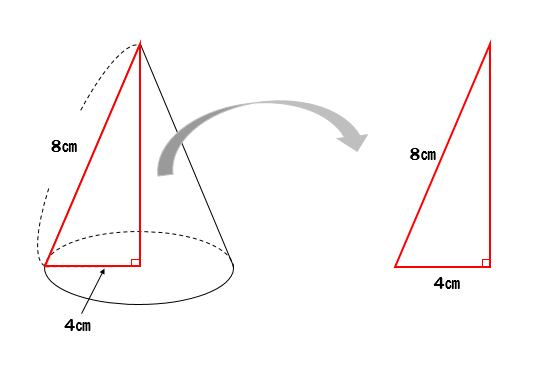
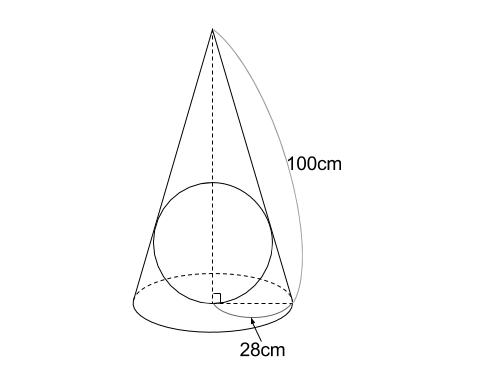
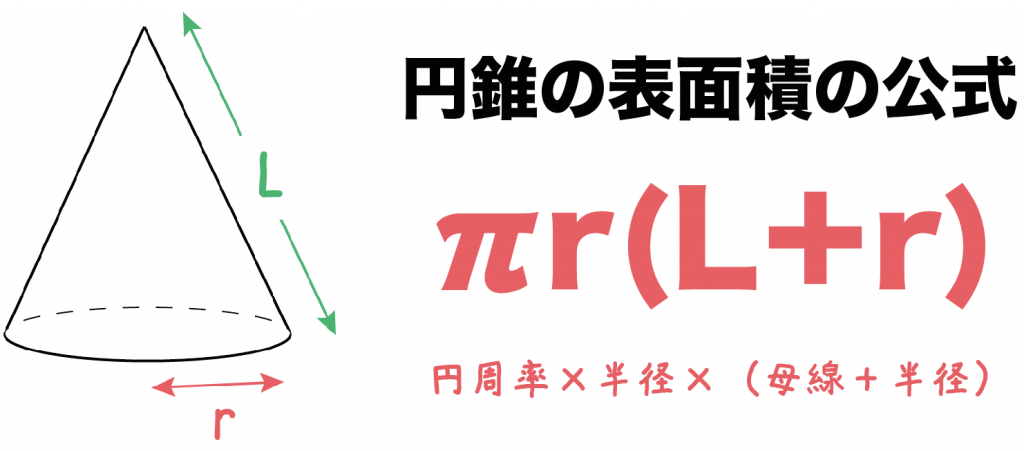
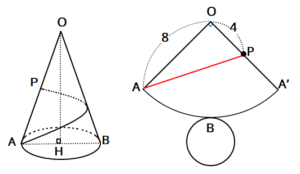
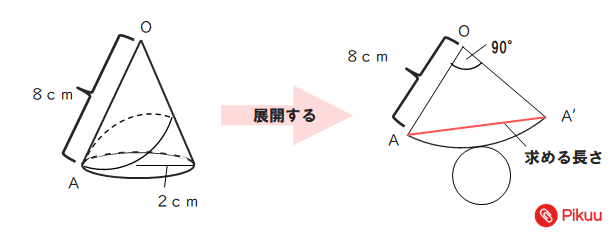
Step3 「三平方の定理」で母線の長さを求める! つぎに、「母線」、「底面の半径」、「円錐の高さ」をふくむ直角三角形をさがそう。例でいうと、 三角形ABOだね。斜辺以外の辺の長さはわかっているよね??(半径5cm、高さ10cmより) 体積を求める問題では円錐の高さが必要ですが、この問題では直接与えられていないので「三平方の定理」で求めます。 解答 (1) 表面積は底面積とおうぎ形の面積の和である。 底面をなす円の半径は \(3 \ \mathrm{cm}\) であるため、底面積 \(S_1\) は \(S_1 = 3^2 \pi = 9\pi \ (\mathrm{cm}^2)\)
Incoming Term: 三平方の定理 円錐 高さ,




0 件のコメント:
コメントを投稿