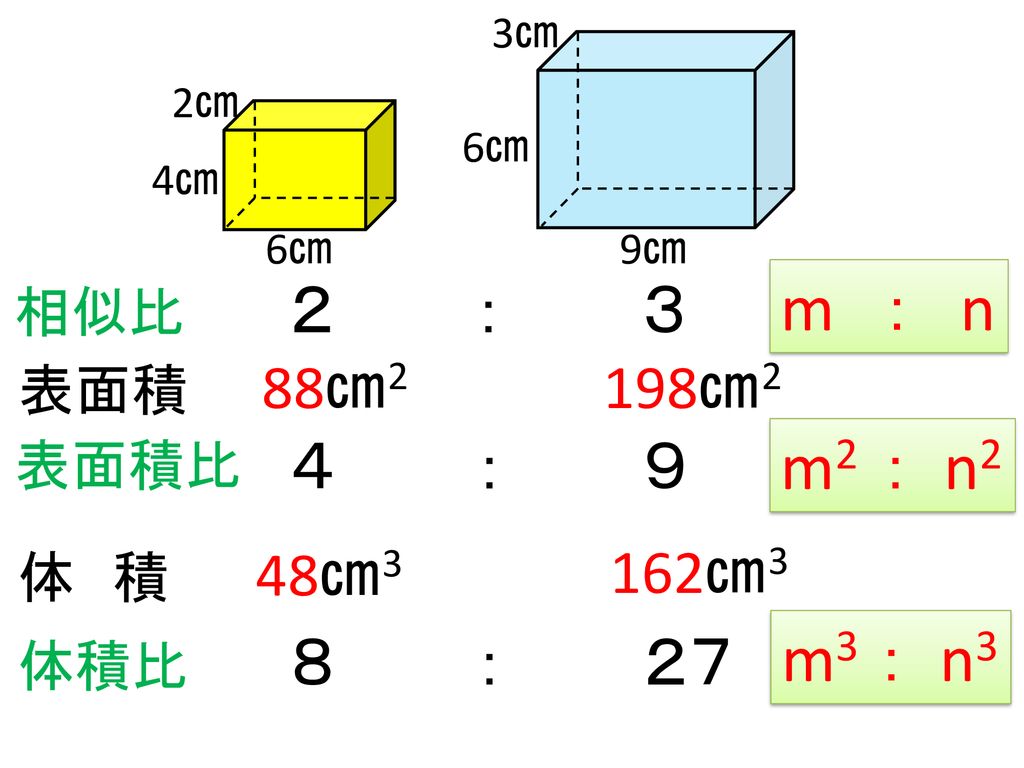
相似な図形の体積比の問題です。基本を確認して、いろいろな応用問題を解けるようにしてください。基本事項相似比が a b である図形の面積の比は, a3 b3である。*簡単な証明もできるようにしましょう。例)1辺の長さaとbの立方体の場合相似比 → ab 体積は a3 と b3 よって上の基面積や体積を相似比をもとにして求めることがで きる。<観察・学習シート> 終 8 末 10 分 ワークの問題を解く。 9 次時の学習内容を知る。 机間指導をする。 、その相似比が :nのとき、面積比はm2:n2 。 相似比と面積比の関係を調べ、角形の相似条件など を,数学の用語や記号 を用いて簡潔に表現す る技能を身に付けてい る。 相似の意味,三角形の 相似条件,平行線と線 分の比についての性 質,相似比と面積比及 び体積比の関係を理解 し,知識を身に付けて いる。 4 単元について (1
相似と体積比 2 ネット塾
相似比 体積比 指導案
相似比 体積比 指導案-相似比 体積比 三角錐 を含む例文一覧と使い方 該当件数 10件 相似な図形の面積比の問題です。基本を確認して、いろいろな応用問題を解けるようにしてください。基本事項相似比が m n である図形の面積の比は,m2 n2 である。例)下のような相似な三角形がある ABCと A'B'C'の相似比は 1:2面積を求めると ABC=4 A'B'C'=16 面積比は1:4相似比が1:2のとき



中学数学 相似な図形の体積比 中学数学の無料オンライン学習サイトchu Su
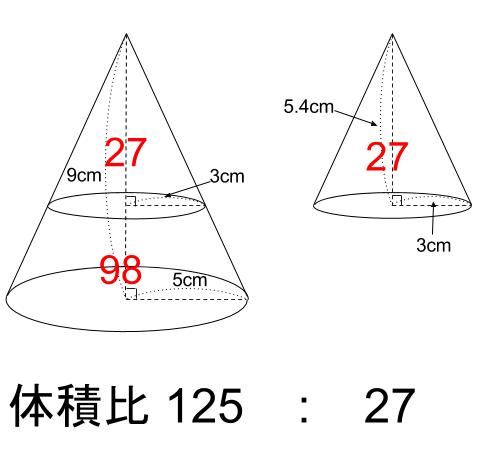
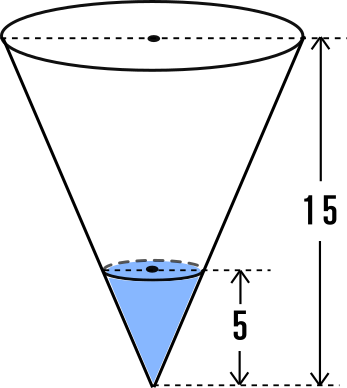
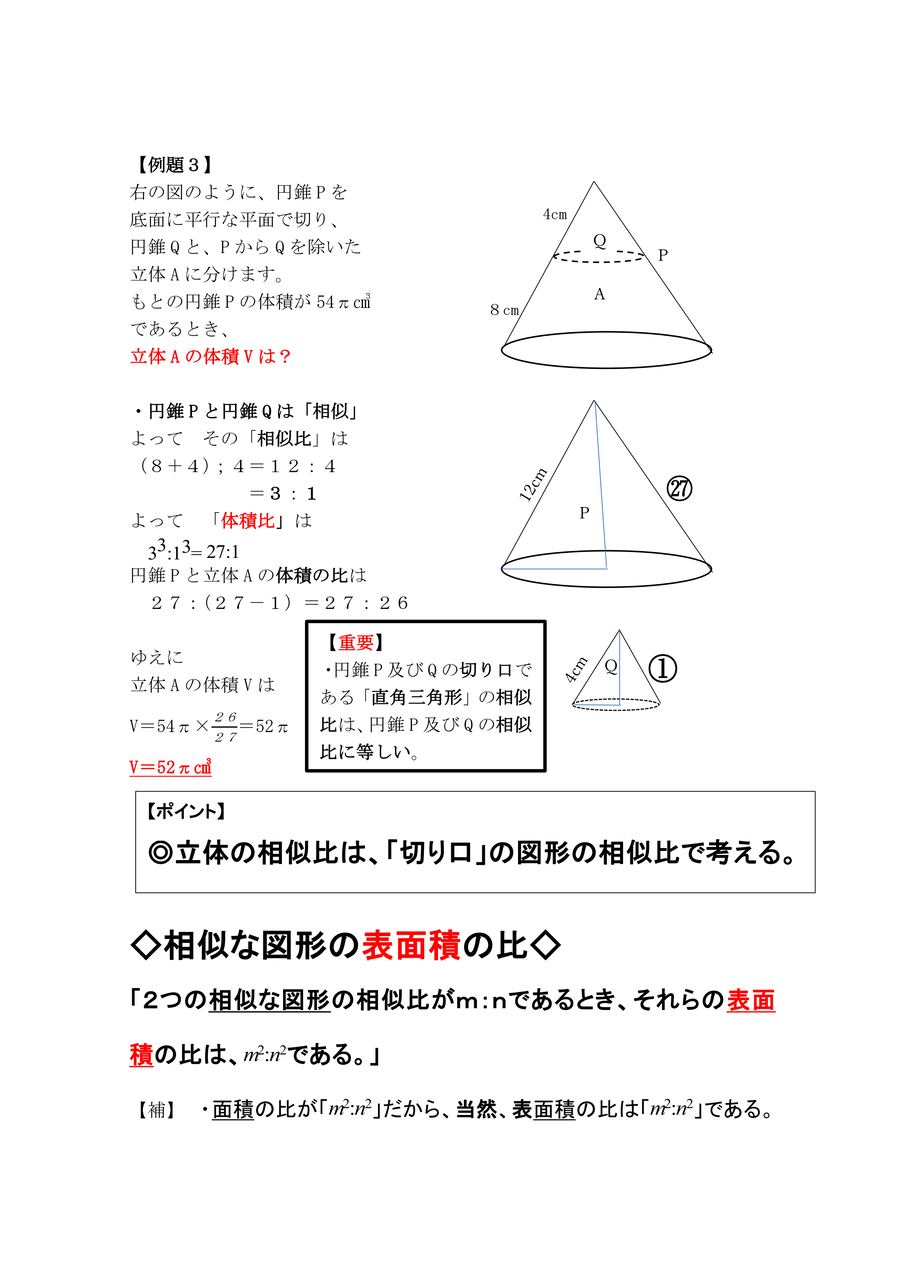
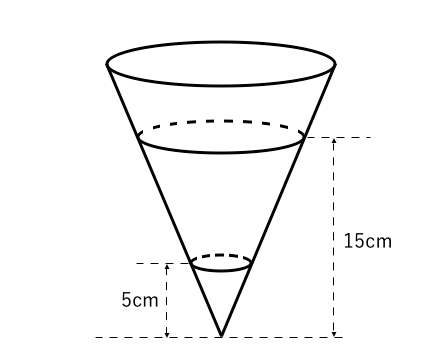
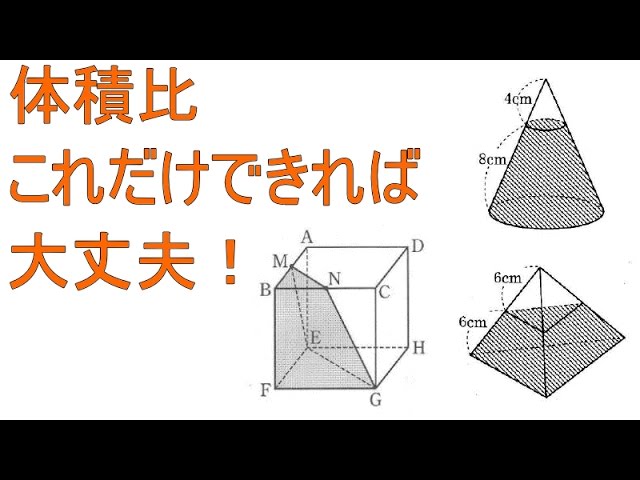
ある相似比27の三角錐では、体積比はいくつになるでしょうか。 解答 上述のように、体積比の求め方は辺の長さの比を3乗すればいいので、2^3:7^3=8:343と変換されました。 今度は逆に体積比から辺の長さの比を求めていきましょう 例題・相似な図形の相似比と面積比及び体積比を調べ,文字式を用いるなどしてそれらの関 係について考えることができる。 (思考・判断・表現) ・相似な図形の性質に関心をもち,それについて考えたり,それを用いて証明したりし ようとしている。相似な空間図形の相似比と面積比,体積比の関係を知り, 使うことができる。 問題 の図ような円錐容器に コップ1杯の水を入れたら, 深さが容器の半分になった。 この容器を満水にするにはあ と何杯必要ですか。 文字を用いて一般的に相 似比と面積
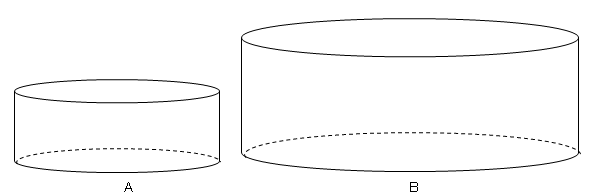
中学校3年相似な図形の面積と体積2/4時間・相似な図形17/時間(東京書籍新しい数学3p 14 ) 思考の開始 ・相似比は 3:5 ・周の長さの比 3:5 ・面積比は 32:52=9:25 思考の取り出し 問題 ☆記述のポイント!相似な円柱の表面積比・体積比 下記のように相似な2つの円柱があったとします。(相似比は1:k) この2つの円柱の表面積比と体積比を比べてみましょう。 図のように、左の円柱の底面の円の半径をr、高さをhとしたときに、相似比は1:kであることから、ウ 平行線と線分の比についての性質を見いだし、それらを確かめること。 エ 基本的な立体の相似の意味と、相似の図形の相似比と面積比及び体積比の関係に ついて理解すること。 オ 相似な図形の性質を具体的な場面で活用すること。
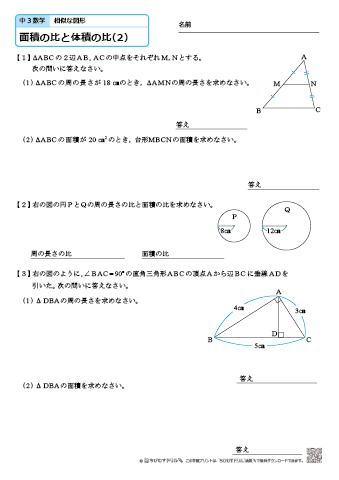
体積比1 名前 相似比が の相似な2つの三角錐がある。 2つの三角錐の体積比を求めなさい。 右の図のような相似である円柱a,bがある。 次の問いに答えなさい。 ①円柱a,bの表面積の比を求めなさい。 ②円柱a,bの体積の比を求めなさい。・大小のケーキの相似比から体積比を求め,値段と比較する。 ・大きいケーキ1個分と小さいケーキ3個の体積を計算して求 め,値段と比較する。 3 どちらの買い方が得になるか,見通しに基づいて 自力解決をする。 4 全体で,求め方について話し合う。全体の相似比は1:2であり,そ の体積比は13:23=1:8であ る。つまり,ジュースの入っている部分と 入っていない上の部分の体積比は1:7である。 よって,あと7杯分入れるとよい。 答 7杯分



2つの球の半径がそれぞれ5cm 2cmのとき相似比表面積比体積 Yahoo 知恵袋



热烈欢迎各位专家 同行光临指导 Ppt Download
②体積の比 Pの体積 2r×2r×π×2h=8πr 2 h Qの体積 3r×3r×π×3h=27πr 2 h 体積の比 8πr 2 h27πr 2 h=7 確認 答表示 円錐Aと円錐Bは相似で、相似比は34である。 AとBの表面積の比を求めよ。 916 AとBの体積の比を求めよ。 2764 円柱Cと円柱Dは相似で、表面積の比が9まず相似比を求める P:もと=2 3 p:もと=22:32 =4:9 次に表面積比を求める (イ) pとqの体積比を求めよ。 まずpともとの立体の体積比を求める P:もと=23 33 =8 27 次のqの体積比を求める。 もと -p 体積比27 体積比8 =q 体積比19相似における測度的側面に関しては,中 点連結定 理の図に中点lを 加えて,図 中に存在する三角形の面積を考える中で,相 似比と面積比を考えた。また, 大きさの異なる2つの円錐の体積を比べる中で,相 似比と体積比を考えた。




7 相似比 面積比 体積比 うえまえ先生の数塾 Youtube



中学3年生 数学 面積の比と体積の比 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生
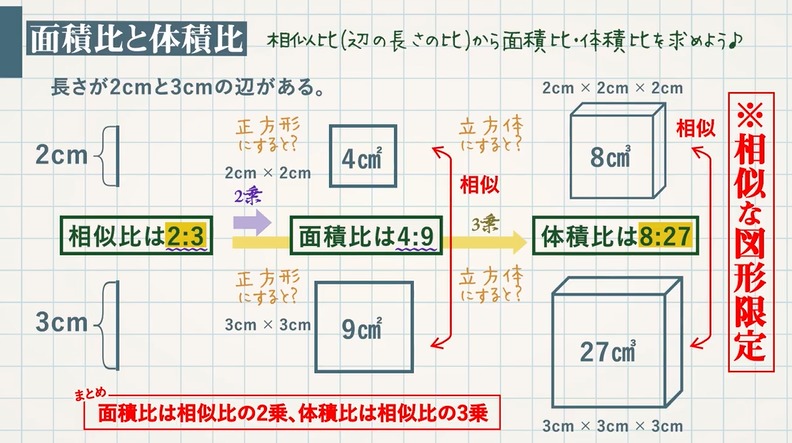
『相似な図形』の単元の中から 平行線と線分の比という内容について解説してきます。 ここでは、相似な図形の性質をつかって いろんな図形の辺の長さを求めていきます。 長々と解説をするよりも 問題を見ながら、実践を通して学習するのが良いので相似比(辺の長さの比)から 面積比 と 体積比 を求めましょう。 長さ $2\rm cm$ と $3\rm cm$ の辺があります。この $2$ 辺の長さの比 (相似比)は $\textcolor{blue}{23}$ になります。 正方形にしてそれぞれの面積を考えると、 $1$ 辺の長さが $2 \rm cm2×2(2\textcolor{blue} 相似比から面積比をだす 相似比が出ちゃえばあとは簡単。 相似比を2乗すれば面積比がでるってわけ。 abcと a'b'c'の相似比は、 1 2 だったね?? 面積比は2乗してやった比の、 1² 2² = 1 4 になるはず! おめでとう! 相似比から面積比を計算でき




面積比と体積比 教遊者




木星的體積比最小的恆星還要大 為什麼它不能成為恆星呢 中國熱點
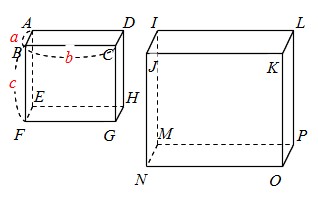
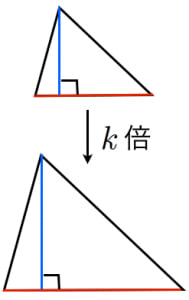
空間図形の表面積比と体積比 右の図のように、2つの立体が相似ならば、対応する表面の図形も互いに相似である。 それゆえ、相似比が m n の図形の表面比は S S ′ = m 2 n 2 となる。 また、左の三角推の底面積と高さを T 、 h とすると、右の三角錐の底相似な立体で,相似比がm:n ならば,表面積の比はm 2:n 2,体積の比はm 3:n 3である。 3 (1) 3:2 ポイント FとGは相似な立体だから,底面の半径の比も3:2と の長さの比は,底面の半径の比に等しく3:2となるね。 (2) 56cm2 ポイントエ 基本的な立体の相似の意味と,相似な図形の相似比と面積比及び体積比の関係について理解す ること。 オ 相似な図形の性質を具体的な場面で活用すること。 本単元における本質的な問い ・ 2つの三角形が相似であるためには,どのような条件が




質問です Clear




3分でわかる 相似比から体積の比 表面積比を求める公式 Qikeru 学びを楽しくわかりやすく
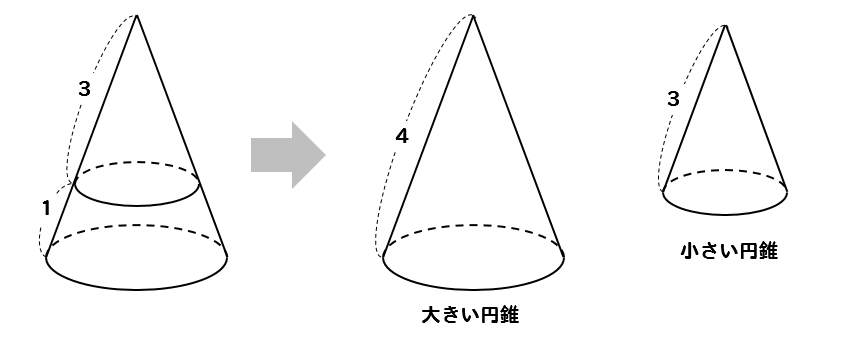
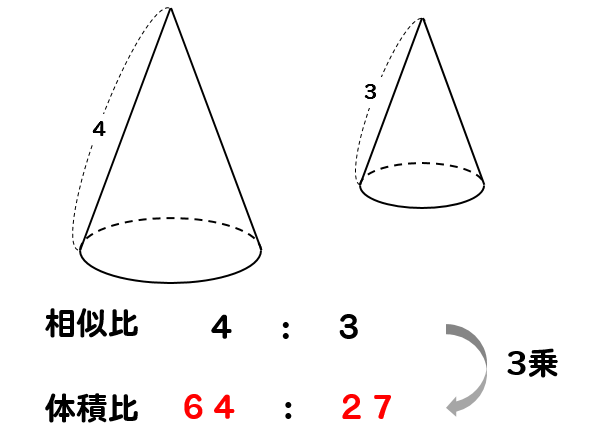
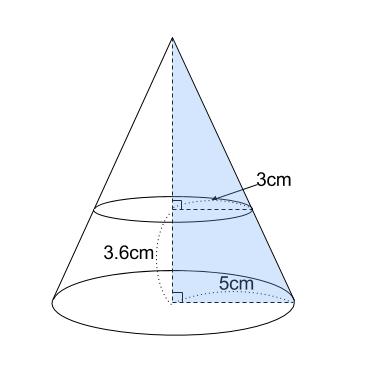
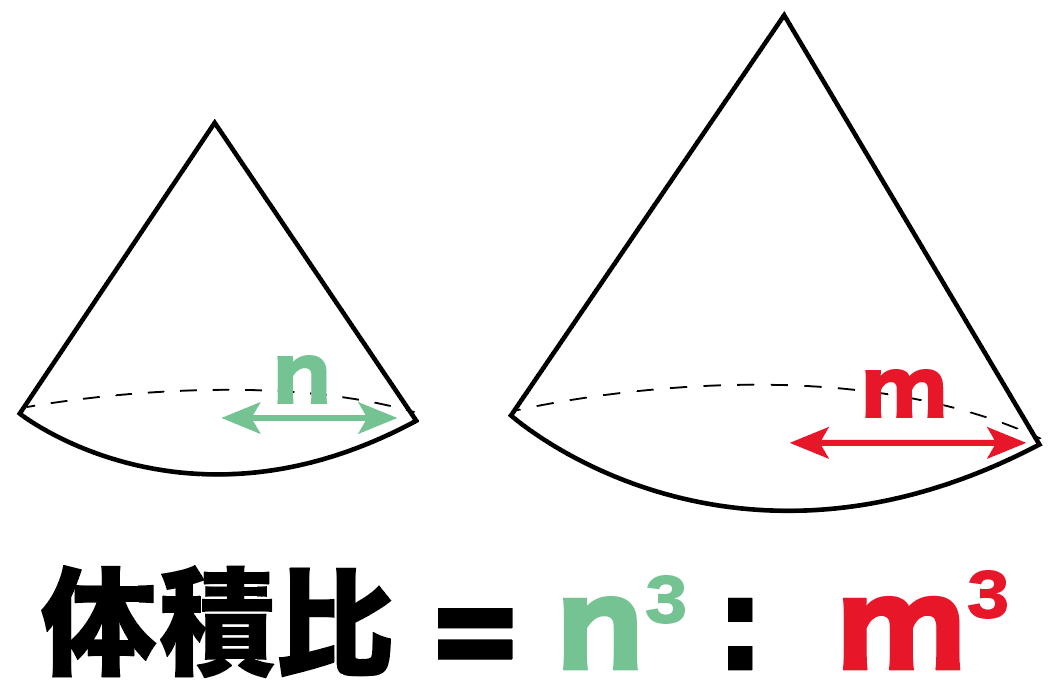
:n ならば 面積比は、m2:n2 である。 ② 相似な立体の表面積比は、相似比の2乗に等しい。 相似比がm:②基本的な立体の相似の意味及び相似 な図形の相似比と面積比や体積比と の関係について理解している。 ③相似な図形の相似比を求めたり,相似 な図形の辺の長さや面積,体積を,相 似比を基にして求めたりすることが できる。 相似比を3乗することで求めてやることができます。 つまり 相似比がわかれば 体積比はすーぐに求めることができるということですね! それでは、さっきの円錐の問題を考えてみましょう。 円錐問題の考え方 円錐を2つに分けた図形の体積比を考えるの




中3 数学 相似15 表面積比 体積比 9分 Youtube




3分でわかる 相似比から体積の比 表面積比を求める公式 Qikeru 学びを楽しくわかりやすく




動画で学習 3 相似な立体の表面積の比 体積の比 数学



相似 面積 比 応用




図形の面積比 体積比 数学i フリー教材開発コミュニティ Ftext




中学数学 相似な図形の体積比 中学数学の無料オンライン学習サイトchu Su



Studydoctor相似比と体積の計算 円錐台 三角錐台 中学3年数学 Studydoctor




3分でわかる 相似比から体積の比 表面積比を求める公式 Qikeru 学びを楽しくわかりやすく




相似立体图形体积比 立体图形有没有相似 如果相似 体积比能否等于相似比的立方 三人行教育网 Www 3rxing Org



Math 空間図形と相似 面積比 体積比 発展問題 働きアリ The 2nd
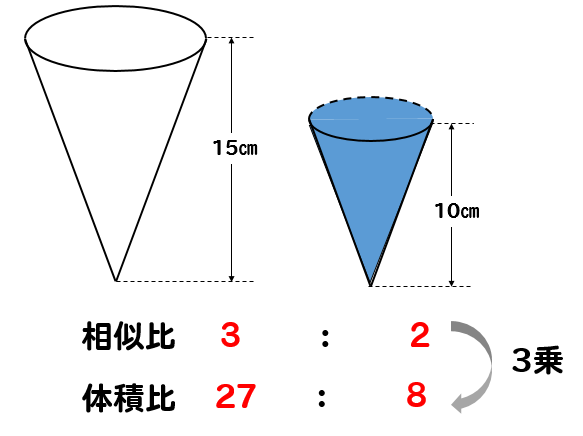



中学数学 円錐の体積比を相似を使って求める方法を問題解説 数スタ
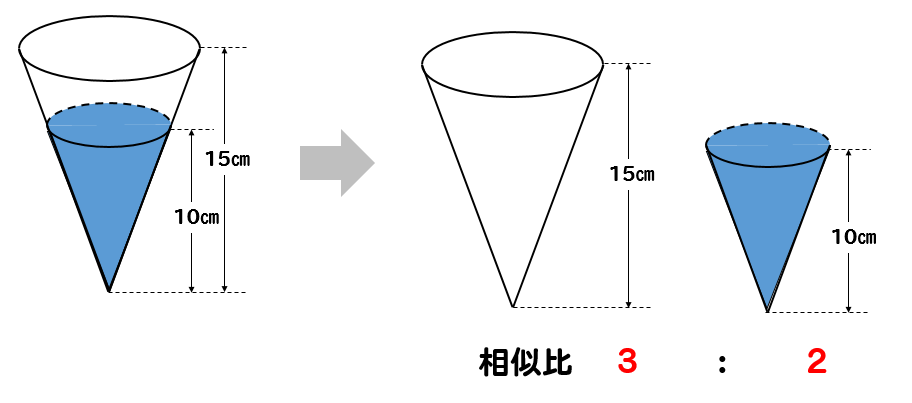



中学数学 円錐の体積比を相似を使って求める方法を問題解説 数スタ




Ayaka 緋弾済 على تويتر 相似な図形の面積比 体積比 相似比 長さの比 A B 面積比a B 底面積比 表面積比でも 体積比a B 相似な図形のときしか使えないことに注意 T Co 2aieisbrjd
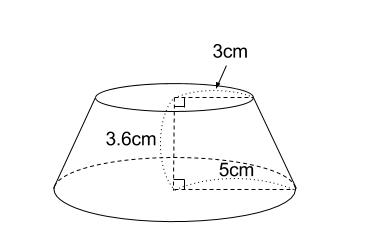



中学数学 相似な図形の体積比 中学数学の無料オンライン学習サイトchu Su
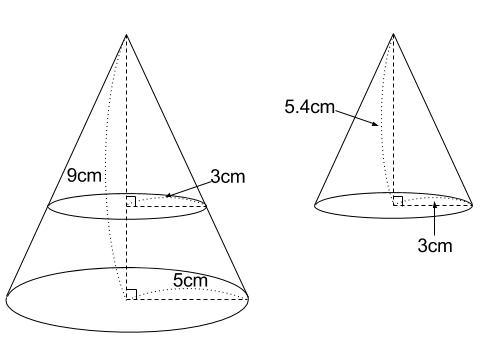



中学数学 相似な図形の体積比 中学数学の無料オンライン学習サイトchu Su




面積比と体積比 教遊者




中学数学 円錐の体積比を相似を使って求める方法を問題解説 数スタ




数学所有体积公式




3分でわかる 相似比から体積の比 表面積比を求める公式 Qikeru 学びを楽しくわかりやすく



Math 相似比 面積比 体積比 面積比が2乗 体積比が3乗になる証明 働きアリ




中3 数学相似比 ニスヌーピー壁紙
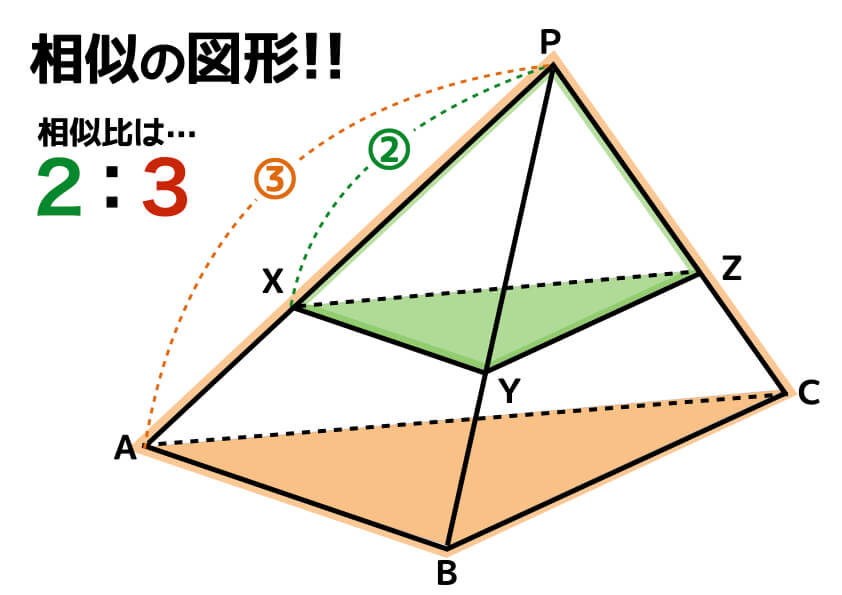



小学生でもスッキリ理解できる 体積比のコツと求め方 中学受験ナビ



相似 比 求め 方



Http Www Pref Osaka Lg Jp Attach 6629 Jmw 3b5 10 Pdf




面積比の公式まとめ 相似比と面積比と体積比の関係もあわせて解説 遊ぶ数学



Math Page



22年云南省公务员数资知识点 几何问题中相似比的运用 公务员考试网 华图教育




相似な直方体の表面積比 体積比 中学数学 By Okボーイ マナペディア



特斯拉全新suv 体积比model 3 还大 3 9万美元起售 品牌




相似な円柱の表面積比 体積比 中学数学 By Okボーイ マナペディア




相似比と体積比 無料で使える中学学習プリント



Www Takwing Idv Hk Studyroom Ce Maths Teaching Basic V3 18 Area N Vol 8 Pdf




中学数学 円錐の体積比を相似を使って求める方法を問題解説 数スタ




相似比 面積比 体積比 一新ゼミ 金沢市にある小学生 中学生 高校生対象の塾



巧用相似解实际问题 29 1形状相同的图形 初中冀教版 数学中国网



高校入試 英語 数学 図形と相似 面積比と体積比




覚えて損はない 相似な立体同士の3つの性質 Qikeru 学びを楽しくわかりやすく




相似比与体积比的关系 相似体体积比等于什么 急用 三人行教育网 Www 3rxing Org




中学校数学 証明のコツ 面積比 体積比



中学3年数学練習問題 相似な立体の表面積と体積の比 図形と相似



中学校数学 証明のコツ 面積比 体積比




相似比と体積比 無料で使える中学学習プリント



受動態 相似比 面積比 体積比 今日の板書



中学数学 円錐の体積比を相似を使って求める方法を問題解説 数スタ




図形の面積比 体積比 数学i フリー教材開発コミュニティ Ftext




山形県 入試対策 数学 遠tからの挑戦状 相似比 体積比




中3数学 相似な図形の表面積比 体積比 練習編 映像授業のtry It トライイット



相似比と面積比 体積比の公式の証明 高校数学の美しい物語
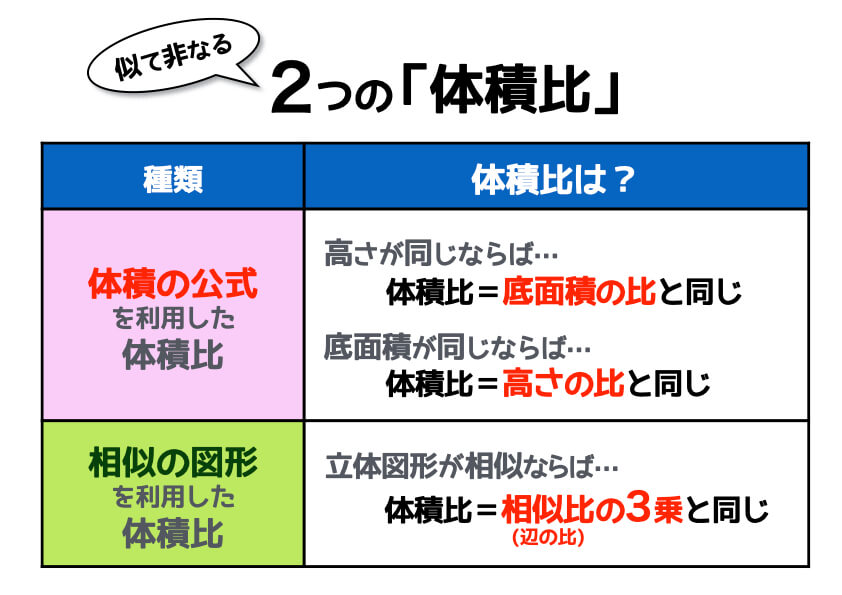



小学生でもスッキリ理解できる 体積比のコツと求め方 中学受験ナビ




中3 三角形の相似 円錐の体積比 日本語版 Youtube



本時の目標 身近な直方体をもとに実際に表面積と体積を求めることで 相似な立体の表面積比と体積比について理解する Ppt Download



相似三角形的面積比與邊長對應關係比 Live 多媒體數學觀念典online




問2 教えてくれたら幸いです Clear
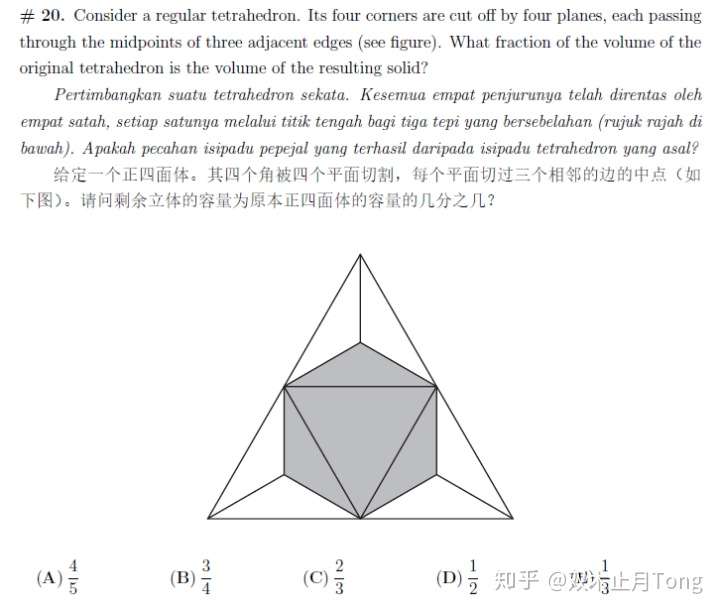



袋鼠数学竞赛真题及解析 三



相似の問題23 テスト 受験対策 苦手な数学を簡単に




相似比と体積比 中学3年生 相似 数学 Youtube




相似と体積比 2 ネット塾
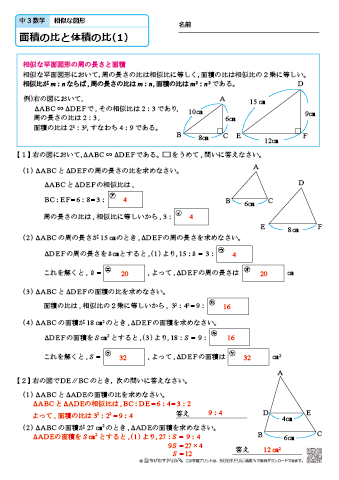



中学3年生 数学 面積の比と体積の比 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生



圆与相似的问题 图片欣赏中心 急不急图文 Jpjww Com



相似比と体積の計算 円錐台 三角錐台 中学3年数学 Youtube




相似比と面積比と体積比の関係を解説 公式を使って面積や体積を求めよう



高校入試 英語 数学 図形と相似 面積比と体積比




空間図形12 相似比面積比体積比 Youtube



中学数学 円錐の体積比を相似を使って求める方法を問題解説 数スタ



Math 空間図形と相似 面積比 体積比 発展問題 働きアリ




中学校数学 証明のコツ 面積比 体積比



相似な立体 中学3年 数学クラブ
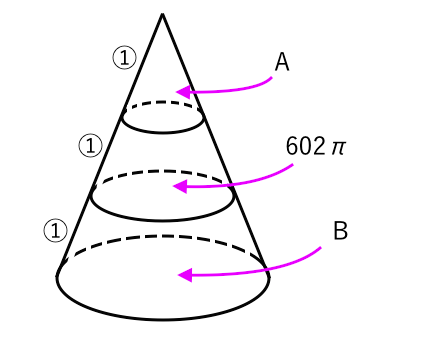



相似な図形 体積比 相似な図形に注目せよ 苦手な数学を簡単に




Ratio Of Areas And Volumes Of Similar Figures 相似圖形的面積比和體積比 Geogebra



面積比と体積比 教遊者



4 13 相似比 表面積比 面積比を求めるには さんすうがく パート 2



相似な図形 体積比 相似な図形に注目せよ 苦手な数学を簡単に




図形の面積比 体積比 数学i フリー教材開発コミュニティ Ftext



中学数学 相似な図形の体積比 中学数学の無料オンライン学習サイトchu Su



3分でわかる 相似比から体積の比 表面積比を求める公式 Qikeru 学びを楽しくわかりやすく



相似三角形的性质 相似ppt 第一ppt
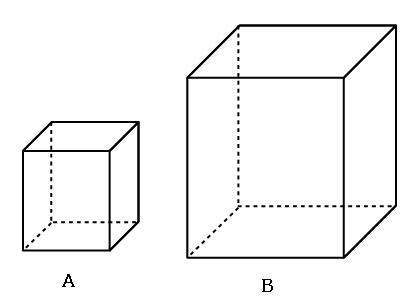



相似比と面積比と体積比の関係を解説 公式を使って面積や体積を求めよう
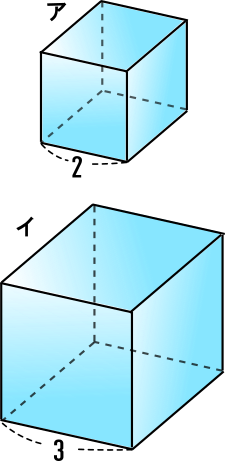



中学3年数学練習問題 図形と相似 相似な立体の表面積と体積の比
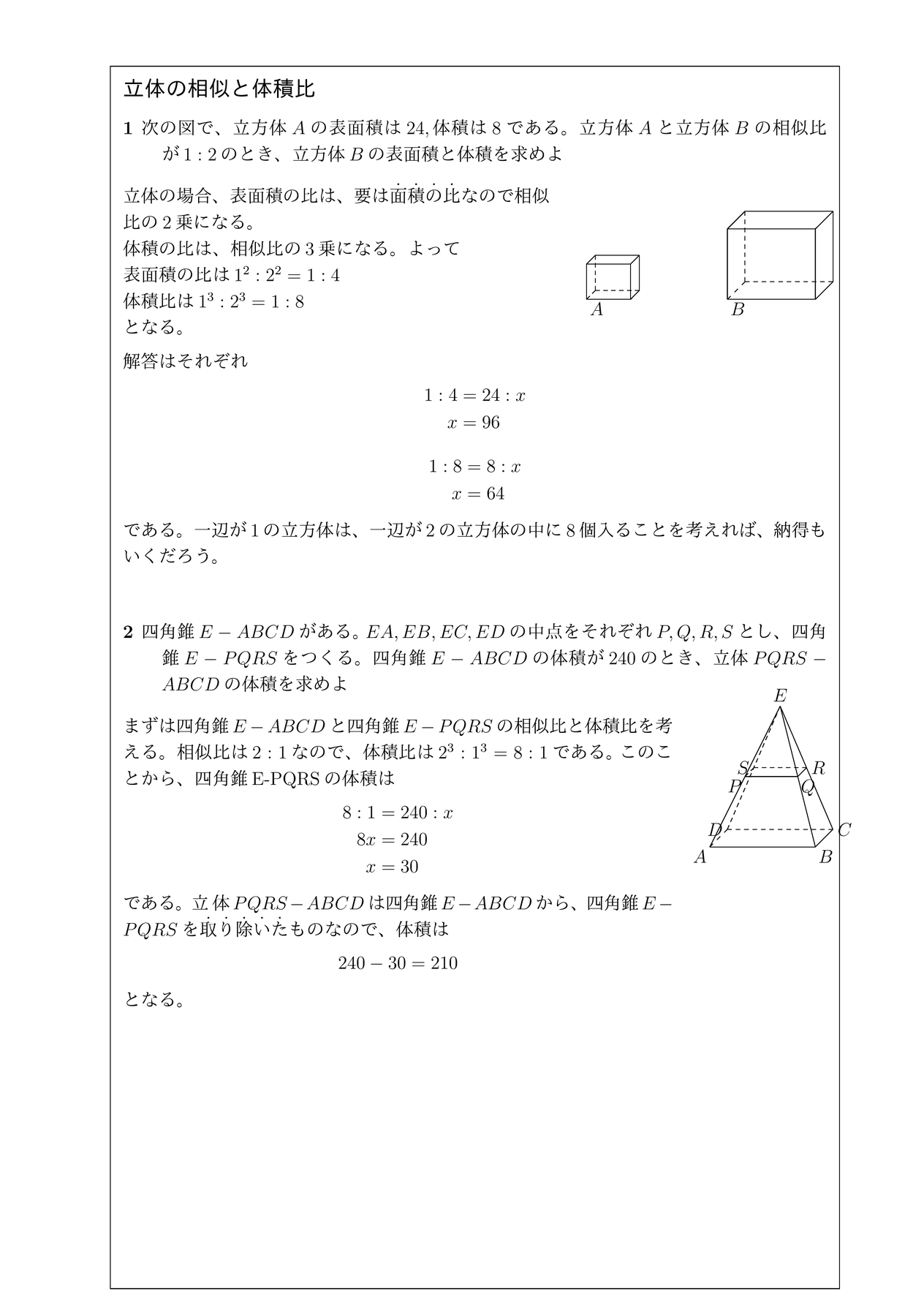



立体の相似と表面積比 体積比 チーム エン



Math 相似比 面積比 体積比 面積比が2乗 体積比が3乗になる証明 働きアリ



受動態 相似比 面積比 体積比 今日の板書




10 面積比 体積比 球の表面積と体積
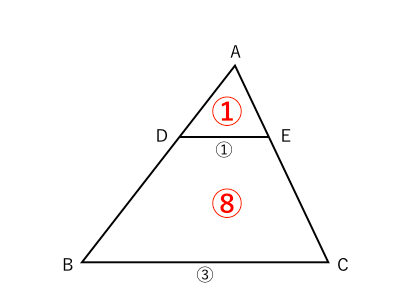



相似比と面積比と体積比はお友だち 苦手な数学を簡単に




立方定律 兩個幾何形狀相似物體對應長度比為a B 則對應體積比為a 3 百科知識中文網




あってますか 面積比 Clear




3分でわかる 相似比から体積の比 表面積比を求める公式 Qikeru 学びを楽しくわかりやすく
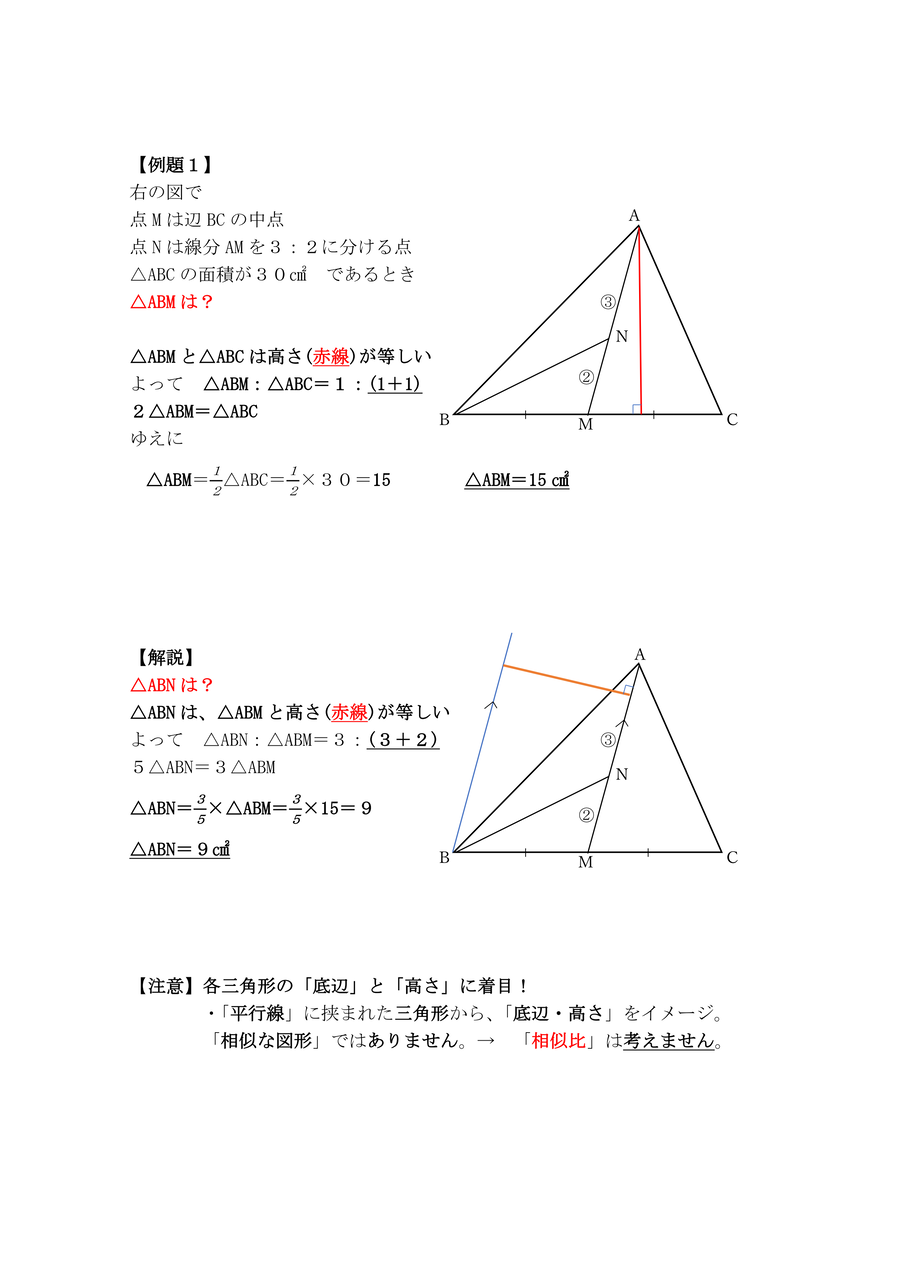



中学校数学 証明のコツ 面積比 体積比
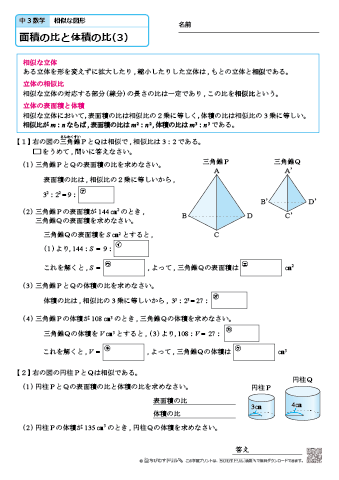



中学3年生 数学 面積の比と体積の比 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生



Studydoctor予習 テスト勉強前に 10分で丸わかり相似比と面積比 体積比まとめ 中学3年数学 Studydoctor



体積 の 比 の 求め 方




数学 中3 54 相似と体積 基本編 Youtube




中3数学 相似な図形の表面積比 体積比 映像授業のtry It トライイット




中三 面積和體積 相似形狀對應邊的比與體積的比之關係 Youtube
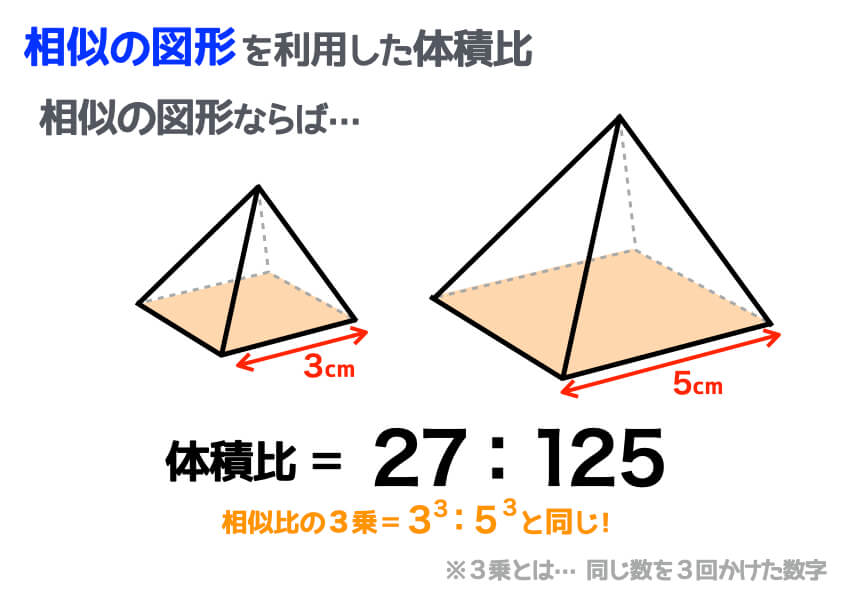



小学生でもスッキリ理解できる 体積比のコツと求め方 中学受験ナビ




相似比と体積比 円錐台 中学3年数学 Youtube



相似 比 問題



0 件のコメント:
コメントを投稿